■Zhang, Z., Konno, K., Tokuyama, Y., Curve Mesh Reconstruction Based on Mountain Contours, The Journal of ITE, Vol.60, No.11, pp.1803-1810, (2006).

Abstract:
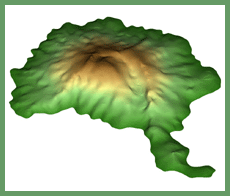
The need for ways to obtain highly accurate 3D shape data from existing 2D contours is increasingly necessary in some applications, such as in disaster prevention, environmental analysis, and creating construction plans. In this paper, we propose an algorithm that reconstructs a curve mesh model of mountain with triangular and quadrilateral domains that is generated from discrete contours data by using constrained Delaunay triangulation method. To prove the e.ectiveness of our method, we interpolated the curve mesh into free-form surface model with G1 continuity and compared the accuracy and quantity of data with other methods.

■Zhang, Z., Konno, K., Tokuyama, Y., 3D Terrain Reconstruction Based on Contours, Ninth International Conference on Computer Aided Design and Computer Graphics (CAD/CG 2005) , pp.325-330, (2005).

Abstract:
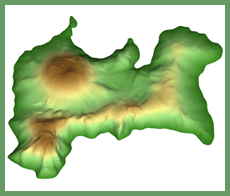
In 3D terrain reconstruction, the differences of shape and topology among contours in adjacent sections cause a difficulty as the tiling problem of branching terrain. In this paper, we present a brief and pure geometrical algorithm to reconstruct 3D terrain based on contours. The merit of our method is that the tiling rules guarantee arbitrary branching terrain can be divided into correct topology.

■Zhang, Z., Konno, K., and Tokuyama, Y., 3D Model Generation of Mountain Terrain Based on Periodic B-Spline Curves, Proc. NICOGRAPH INTERNATIONAL 2004, pp.31-36, (2004).

Abstract:
In geographic information system, 3D geographical data is prerequisite basic data for digital map, car navigation system, disaster prevention and so on. As one of representation methods of geographical data, DEM (digital elevation model) is defined as a regular grid matrix of elevation values that represent geographic shape. In this paper, we present a procedure to construct a set of B-spline surfaces based on contour lines obtained from DEM.